让你立刻爱上数学的10个算术游戏
来源:未知发布时间:2019-07-15
恣意选一个四位数（数字不能全相同），把一切数字从大到小排列，再把一切数字从小到大排列，用前者减去后者得到一个新的数。反复对新得到的数停止上述操作，7 步以内必然会得到 6174。
例如，选择四位数 6767：
7766 - 6677 = 1089
9810 - 0189 = 9621
9621 - 1269 = 8352
8532 - 2358 = 6174
7641 - 1467 = 6174
……
6174 这个“黑洞”就叫做卡普雷卡尔（Kaprekar）常数。关于三位数，也有一个数字黑洞——495。
3x + 1 问题
恣意选一个四位数（数字不能全相同），把一切数字从大到小排列，再把一切数字从小到大排列，用前者减去后者得到一个新的数。反复对新得到的数停止上述操作，7 步以内必然会得到 6174。
例如，选择四位数 6767：
7766 - 6677 = 1089
9810 - 0189 = 9621
9621 - 1269 = 8352
8532 - 2358 = 6174
7641 - 1467 = 6174
……
6174 这个“黑洞”就叫做卡普雷卡尔（Kaprekar）常数。关于三位数，也有一个数字黑洞——495。
3x + 1 问题
从恣意一个正整数开端，反复对其停止下面的操作：假如这个数是偶数，把它除以 2 ；假如这个数是奇数，则把它扩展到原来的 3 倍后再加 1 。你会发现，序列最终总会变成 4, 2, 1, 4, 2, 1, … 的循环。
例如，所选的数是 67，依据上面的规则能够依次得到：
67, 202, 101, 304, 152, 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17,
52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, ...
数学家们试了很多数，没有一个能逃脱“421 圈套”。但是，能否关于 一切 的数，序列最终总会变成 4, 2, 1 循环呢？
这个问题能够说是一个“坑”——乍看之下，问题十分简单，打破口很多，于是数学家们纷繁往里面跳；殊不知进去容易进来难，不少数学家到死都没把这个问题搞出来。
曾经中招的数学家不可胜数，这能够从 3x + 1 问题的各种别名看出来： 3x + 1 问题又叫 Collatz 猜测、 Syracuse 问题、 Kakutani 问题、 Hasse 算法、 Ulam 问题等等。
后来，由于命名争议太大，痛快让谁都不沾光，直接叫做 3x + 1 问题算了。
直到如今，数学家们依然没有证明，这个规律关于一切的数都成立。
从恣意一个正整数开端，反复对其停止下面的操作：假如这个数是偶数，把它除以 2 ；假如这个数是奇数，则把它扩展到原来的 3 倍后再加 1 。你会发现，序列最终总会变成 4, 2, 1, 4, 2, 1, … 的循环。
例如，所选的数是 67，依据上面的规则能够依次得到：
67, 202, 101, 304, 152, 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17,
52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, ...
数学家们试了很多数，没有一个能逃脱“421 圈套”。但是，能否关于 一切 的数，序列最终总会变成 4, 2, 1 循环呢？
这个问题能够说是一个“坑”——乍看之下，问题十分简单，打破口很多，于是数学家们纷繁往里面跳；殊不知进去容易进来难，不少数学家到死都没把这个问题搞出来。
曾经中招的数学家不可胜数，这能够从 3x + 1 问题的各种别名看出来： 3x + 1 问题又叫 Collatz 猜测、 Syracuse 问题、 Kakutani 问题、 Hasse 算法、 Ulam 问题等等。
后来，由于命名争议太大，痛快让谁都不沾光，直接叫做 3x + 1 问题算了。
直到如今，数学家们依然没有证明，这个规律关于一切的数都成立。
特殊两位数乘法的速算
特殊两位数乘法的速算
假如两个两位数的十位相同，个位数相加为 10，那么你能够立刻说出这两个数的乘积。假如这两个数分别写作 AB 和 AC，那么它们的乘积的前两位就是 A 和 A + 1 的乘积，后两位就是 B 和 C 的乘积。
比方，47 和 43 的十位数相同，个位数之和为 10，因此它们乘积的前两位就是 4×(4 + 1)=20，后两位就是 7×3=21。也就是说，47×43=2021。
相似地，61×69=4209，86×84=7224，35×35=1225，等等。
这个速算办法背后的缘由是，(10 x + y) (10 x + (10 - y)) = 100 x (x + 1) + y (10 - y) 对恣意 x 和 y 都成立。
幻方中的幻“方”
假如两个两位数的十位相同，个位数相加为 10，那么你能够立刻说出这两个数的乘积。假如这两个数分别写作 AB 和 AC，那么它们的乘积的前两位就是 A 和 A + 1 的乘积，后两位就是 B 和 C 的乘积。
比方，47 和 43 的十位数相同，个位数之和为 10，因此它们乘积的前两位就是 4×(4 + 1)=20，后两位就是 7×3=21。也就是说，47×43=2021。
相似地，61×69=4209，86×84=7224，35×35=1225，等等。
这个速算办法背后的缘由是，(10 x + y) (10 x + (10 - y)) = 100 x (x + 1) + y (10 - y) 对恣意 x 和 y 都成立。
幻方中的幻“方”
一个“三阶幻方”是指把数字 1 到 9 填入 3×3 的方格，使得每一行、每一列和两条对角线的三个数之和正好都相同。下图就是一个三阶幻方，每条直线上的三个数之和都等于 15。
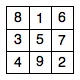
大家或许都听说过幻方这玩意儿，但不晓得幻方中的一些美好的性质。例如，恣意一个三阶幻方都满足，各行所组成的三位数的平方和，等于各行逆序所组成的三位数的平方和。关于上图中的三阶幻方，就有
816² + 357² + 492² = 618² + 753² + 294²
应用线性代数，我们能够证明这个结论。
自然构成的幻方
从 1/19 到 18/19 这 18 个分数的小数循环节长度都是 18。把这 18 个循环节排成一个 18×18 的数字阵，恰恰构成一个幻方——每一行、每一列和两条对角线上的数字之和都是 81
（注：严厉意义上说它不算幻方，由于方阵中有相同数字）。
196 算法
一个“三阶幻方”是指把数字 1 到 9 填入 3×3 的方格，使得每一行、每一列和两条对角线的三个数之和正好都相同。下图就是一个三阶幻方，每条直线上的三个数之和都等于 15。
大家或许都听说过幻方这玩意儿，但不晓得幻方中的一些美好的性质。例如，恣意一个三阶幻方都满足，各行所组成的三位数的平方和，等于各行逆序所组成的三位数的平方和。关于上图中的三阶幻方，就有
816² + 357² + 492² = 618² + 753² + 294²
应用线性代数，我们能够证明这个结论。
自然构成的幻方
从 1/19 到 18/19 这 18 个分数的小数循环节长度都是 18。把这 18 个循环节排成一个 18×18 的数字阵，恰恰构成一个幻方——每一行、每一列和两条对角线上的数字之和都是 81
（注：严厉意义上说它不算幻方，由于方阵中有相同数字）。
196 算法
一个数正读反读都一样，我们就把它叫做“回文数”。随意选一个数，不时加上把它反过来写之后得到的数，直到得出一个回文数为止。例如，所选的数是 67，两步就能够得到一个回文数 484：
67 + 76 = 143
143 + 341 = 484
把 69 变成一个回文数则需求四步：
69 + 96 = 165
165 + 561 = 726
726 + 627 = 1353
1353 + 3531 = 4884
89 的“回文数之路”则特别长，要到第 24 步才会得到第一个回文数，8813200023188。
大家或许会想，不时地“一正一反相加”，最后总能得到一个回文数，这当然屡见不鲜了。事实状况也的确是这样——关于 简直 一切的数，依照规则不时加下去，迟早会呈现回文数。
不过，196 却是一个相当引人瞩目的例外。数学家们曾经用计算机算到了 3 亿多位数，都没有产生过一次回文数。从 196 动身，终究能否加出回文数来？196 终究特殊在哪儿？这至今仍是个谜。
Farey 序列
选取一个正整数 n。把一切分母不超越 n 的 最简 分数找出来，从小到大排序。这个分数序列就叫做 Farey 序列。例如，下面展现的就是 n = 7 时的 Farey 序列。
定理：在 Farey 序列中，关于恣意两个相邻分数，先算出前者的分母乘以后者的分子，再算出前者的分子乘以后者的分母，则这两个乘积一定正好相差1 ！
这个定理有从数论到图论的各种证明。以至有一种证明办法巧妙地借助 Pick 定理，把它转换为了一个不证自明的几何问题！
独一的解
经典数字谜题：用 1 到 9 组成一个九位数，使得这个数的第一位能被 1 整除，前两位组成的两位数能被 2 整除，前三位组成的三位数能被 3 整除，以此类推，不断到整个九位数能被 9 整除。
没错，真的有这样猛的数：381654729。其中 3 能被 1 整除，38 能被 2 整除，381 能被 3 整除，不断到整个数能被 9 整除。这个数既能够用整除的性质一步步推出来，也能应用计算机编程找到。
另一个有趣的事实是，在一切由 1 到 9 所组成的 362880 个不同的九位数中，381654729 是独一一个满足请求的数！
数在变，数字不变
123456789 的两倍是 246913578，正好又是一个由 1 到 9 组成的数字。
246913578 的两倍是 493827156，正好又是一个由 1 到 9 组成的数字。
把 493827156 再翻一倍，987654312，照旧恰恰由数字 1 到 9 组成的。
把 987654312 再翻一倍的话，将会得到一个 10 位数 1975308624，它里面依然没有反复数字，恰恰由 0 到 9 这 10 个数字组成。
再把 1975308624 翻一倍，这个数将变成 3950617248，照旧是由 0 到 9 组成的。
不过，这个规律却并不会不断持续下去。继续把 3950617248 翻一倍将会得到 7901234496，第一次呈现了例外。
三个神奇的分数
一个数正读反读都一样，我们就把它叫做“回文数”。随意选一个数，不时加上把它反过来写之后得到的数，直到得出一个回文数为止。例如，所选的数是 67，两步就能够得到一个回文数 484：
67 + 76 = 143
143 + 341 = 484
把 69 变成一个回文数则需求四步：
69 + 96 = 165
165 + 561 = 726
726 + 627 = 1353
1353 + 3531 = 4884
89 的“回文数之路”则特别长，要到第 24 步才会得到第一个回文数，8813200023188。
大家或许会想，不时地“一正一反相加”，最后总能得到一个回文数，这当然屡见不鲜了。事实状况也的确是这样——关于 简直 一切的数，依照规则不时加下去，迟早会呈现回文数。
不过，196 却是一个相当引人瞩目的例外。数学家们曾经用计算机算到了 3 亿多位数，都没有产生过一次回文数。从 196 动身，终究能否加出回文数来？196 终究特殊在哪儿？这至今仍是个谜。
Farey 序列
选取一个正整数 n。把一切分母不超越 n 的 最简 分数找出来，从小到大排序。这个分数序列就叫做 Farey 序列。例如，下面展现的就是 n = 7 时的 Farey 序列。
定理：在 Farey 序列中，关于恣意两个相邻分数，先算出前者的分母乘以后者的分子，再算出前者的分子乘以后者的分母，则这两个乘积一定正好相差1 ！
这个定理有从数论到图论的各种证明。以至有一种证明办法巧妙地借助 Pick 定理，把它转换为了一个不证自明的几何问题！
独一的解
经典数字谜题：用 1 到 9 组成一个九位数，使得这个数的第一位能被 1 整除，前两位组成的两位数能被 2 整除，前三位组成的三位数能被 3 整除，以此类推，不断到整个九位数能被 9 整除。
没错，真的有这样猛的数：381654729。其中 3 能被 1 整除，38 能被 2 整除，381 能被 3 整除，不断到整个数能被 9 整除。这个数既能够用整除的性质一步步推出来，也能应用计算机编程找到。
另一个有趣的事实是，在一切由 1 到 9 所组成的 362880 个不同的九位数中，381654729 是独一一个满足请求的数！
数在变，数字不变
123456789 的两倍是 246913578，正好又是一个由 1 到 9 组成的数字。
246913578 的两倍是 493827156，正好又是一个由 1 到 9 组成的数字。
把 493827156 再翻一倍，987654312，照旧恰恰由数字 1 到 9 组成的。
把 987654312 再翻一倍的话，将会得到一个 10 位数 1975308624，它里面依然没有反复数字，恰恰由 0 到 9 这 10 个数字组成。
再把 1975308624 翻一倍，这个数将变成 3950617248，照旧是由 0 到 9 组成的。
不过，这个规律却并不会不断持续下去。继续把 3950617248 翻一倍将会得到 7901234496，第一次呈现了例外。
三个神奇的分数
1/49 化成小数后等于 0.0204081632 …，把小数点后的数字两位两位断开，前五个数依次是 2、4、8、16、32，每个数正好都是前一个数的两倍。
100/9899 等于 0.01010203050813213455 … ，两位两位断开后，每一个数正好都是前两个数之和（也即 Fibonacci 数列）。
而 100/9801 则等于 0.0102030405060708091011121314151617181920212223 … 。
应用组合数学中的“生成函数”能够圆满地解释这些现象的产生缘由。
1/49 化成小数后等于 0.0204081632 …，把小数点后的数字两位两位断开，前五个数依次是 2、4、8、16、32，每个数正好都是前一个数的两倍。
100/9899 等于 0.01010203050813213455 … ，两位两位断开后，每一个数正好都是前两个数之和（也即 Fibonacci 数列）。
而 100/9801 则等于 0.0102030405060708091011121314151617181920212223 … 。
应用组合数学中的“生成函数”能够圆满地解释这些现象的产生缘由。